矩阵论8：正交投影与最小二乘问题

横看成岭侧成峰

正交投影

定义

设 $V_1,V_2$ 是 Euclid 空间 $V$ 的两个字空间。有向量 $\def\bm{\boldsymbol}\bm \alpha\in V$ ，如果对任意 $\bm\beta\in V_1$ ，都有 $(\bm\alpha,\bm\beta)=0$ ，则称为 $\bm\alpha$ 与子空间 $V_1$ 正交，记为

$$\bm\alpha_1\perp V_1$$

如果对任意 $\bm \alpha\in V_2$ ，都有 $\bm\alpha\perp V_1$ ，则称子空间 $V_1$ 与 $V_2$ 正交，记为

$$V_1\perp V_2$$

$V$ 中所有于子空间 $V_1$ 正交的向量的集合也构成 $V$ 的子空间，称为 $V_1$ 的正交补，记为 $V_1^\perp$ ，即

$$V_1^\perp\equiv \lbrace \bm\alpha\in V|\bm\alpha\perp V_1\rbrace$$

正交分解

设 $V_1$ 是 Euclid 空间 $V$ 的字空间，则存在 $V_1$ 的唯一正交补 $V_1^\perp$ ，使得 $V$ 可以正交分解为

$$V=V_1\oplus V_1^\perp$$

证明大意：设 $\bm\xi_1,…,\bm\xi_n$ 是 $V_1$ 的一组标准正交基础，对任意 $\bm\alpha\in V$ ，令

$$\bm\alpha_1=(\bm\alpha,\bm\xi_1)\bm\xi_1+...+(\bm\alpha,\bm\xi_m)\bm\xi_m,\ \bm\alpha_2=\bm\alpha-\bm\alpha_1$$

则 $\bm\alpha_1\in V_1$ ，且

$$(\bm\alpha_2,\bm\xi_i)=(\bm\alpha,\bm\xi_i)-(\bm\alpha_1,\bm\xi_i)=(\bm\alpha,\bm\xi_i)-(\bm\alpha,\bm\xi_i)=0,\ \forall\ i=1,2,...m$$

故 $\bm\alpha_2\in V_1^\perp$ ，且 $\bm\alpha=\bm\alpha_1+\bm\alpha_2$ ，所以 $V=V_1\oplus V_1^\perp$ 。

同时，称 $\bm\alpha_1$ 是 $\bm\alpha$ 在 $V_1$ 上的正交投影（Orthogonal Projection）。

例：矩阵的列空间 $R(A)$ 和其转置的零空间 $N(A^T)$ 构成一组正交分解

$$\begin{aligned} R(A)^\perp &= \{ \bm\beta|\bm\beta\perp(k_1\bm\alpha_1+...+k_n\bm\alpha_n),\ k_j\in R \}\\ &= \{\bm\beta|\bm\beta\perp\bm\alpha_j,\ j=1,...,n \} \\ &= \{\bm\beta|\bm\alpha_j^T\bm\beta=0,\ j=1,...,n \} \\ &= \{\bm\beta|A^T\bm\beta=0 \} \\ &= N(A^T) \end{aligned}$$

---

最小二乘问题

最小二乘问题除了可以通过分析的角度解决，也可以从几何的角度来思考。

令 $\bm y=A\bm x$ ，显然 $\bm y\in R(A)$ ，因此最小二乘问题即在 $R(A)$ 找出向量 $A\tilde {\bm x}$ ，使得向量 $\bm b$ 到 $A\tilde{\bm x}$ 的距离最短，即 $A\tilde{\bm x}$ 是向量 $\bm b$ 在 $R(A)$ 上的最佳逼近，满足

$$\Vert A\tilde{\bm x}-\bm b \Vert \le \Vert A\bm x-\bm b \Vert ,\quad \forall\ \bm x \in \mathbb R^n$$

最佳逼近定理：

设 $V_1$ 是 Euclid 空间 $V$ 的子空间，则对给定的 $\bm\alpha\in V$ ，$\bm\alpha_1\in V_1$ 是 $\bm\alpha $ 在 $V_1$ 上的最佳逼近的充要条件是

$$\bm\alpha_2\equiv\bm\alpha-\bm\alpha_1\in V_1^\perp$$

即 $\bm\alpha_1$ 是 $\bm\alpha$ 在 $V_1$ 上的正交投影。

证明大意：

对任意 $\bm\beta\in V_1$ ，根据勾股定理有

$$\begin{aligned} \Vert \bm\alpha-\bm\beta \Vert^2&=\Vert (\bm\alpha-\bm\alpha_1)+(\bm\alpha_1-\bm\beta) \Vert^2 \\ &= \Vert (\bm\alpha-\bm\alpha_1)\Vert^2+\Vert(\bm\alpha_1-\bm\beta) \Vert^2\ \\ &\ge \Vert (\bm\alpha-\bm\alpha_1)\Vert^2 \end{aligned}$$

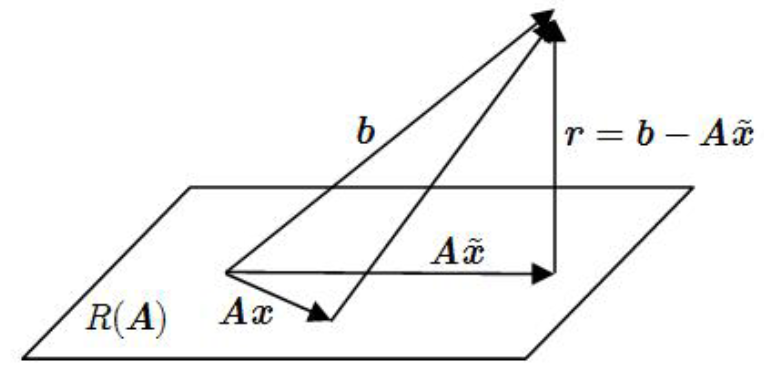
根据最佳逼近定理，这样的最小二乘问题解满足

$$(A\tilde{\bm x}-\bm b)\perp R(A)\\ A^T(A\tilde{\bm x}-\bm b)=0$$

与解析的视角结果一致。